- 사회 연결망 분석은 분석 대상들의 관계를 연결망 구조로 표현하는 분석기법 입니다.
- 주로 친구 관계, 전력 관계를 분석할때 쓰임.
- 사회 연결망 분석을 텍스트 단어 관계에 적용한것이 Semantic Network Analysis
§ 일정한 범위 내에서 동시 등장하는 어휘가 있으면 서로 연결된 것으로 간주하고. 분석한다.

위 그림은 네이버 카페의 리뷰 댓글로 SNA를 진행한 모습이다. 이런식으로 어떤 단어가 의미가 있는지,
다른 단어와 어떤 연관이 있는지 분석할 수 있다.
일정한 범위 내에서 등장하는 어휘를 편하게 알기 위해서, n-gram
import nltk
nltk.download('punkt')
from nltk import word_tokenize, bigrams
sentence 'I love data science and deep learning'
tokens = word_tokenize(sentence)
print(tokens)
>>> ['I', 'love', 'data', 'science', 'and', 'deep', 'learning']
##bigrams : 별도의 함수를 따로 제공
bgram = bigrams(tokens)
print('bgram : ', bgram)
>>> bgram : <generator object bigrams at 0x7efd30ca9dd0>
# 안에 담긴걸 하나씩 풀어서 리스트에 담아야 볼 수 있음.
bgram_list = [x for x in bgram]
print(bgram_list)
>>> [('I', 'love'), ('love', 'data'), ('data', 'science'),
>>> ('science', 'and'), ('and', 'deep'), ('deep', 'learning')]
##trigrams
tgram = ngrams(tokens, 3)
tgram_list = [x for x in tgram]
print(tgram_list)
>>> [('I', 'love', 'data'), ('love', 'data', 'science'), ('data', 'science', 'and'),
>>> ('science', 'and', 'deep'), ('and', 'deep', 'learning')]앞뒤 관계를 파악하기 위한 좋은 방법
어휘 동시 출현 빈도의 계수화
동시 출현(Co-occurrence)
- 2개 이상의 어휘가 일정한 범위나 거리 내에서 함께 출현하는 것을 의미
기능
- 문서나 문장으로부터 두 단어가 유사한 의미를 가졌는지 등의 추상화된 정보를 얻을 수 있음.
- Window지정범위 내에서 동시 등장한 어휘를 확률로 계수화 가능
- 예를 들어, 단어 뒤 잘못된 단어가 온다면, 이를 동시 출현 빈도가 높은 단어로 교정 가능
- 어휘 동시 출현 빈도 행렬은 바이그램 개수를 정리하면 편리하게 만들어 볼 수 있음.
- nltk에서 제공하는 ConditionalFreqDist함수를 이요해서 문맥별 단어빈도를 쉽게 측정 가능..
예시를 들어 해보자.
from nltk import ConditionalFreqDist
sentence = ['I love twice and NewJeans', 'I love twice', 'I like to dance']
tokens = [word_tokenize(x) for x in sentence]
print('tokens : ', tokens)
>>> [['I', 'love', 'twice', 'and', 'NewJeans'],
>>> ['I', 'love', 'twice'],
>>> ['I', 'like', 'to', 'dance']]
bgrams = [bigrams(x) for x in tokens]
print('bigrams : ', bigrams)
>>> bigrams : <function bigrams at 0x7fe508e5bb80>
token = []
for i in bgrams:
token += ([x for x in i])
print('{}번째 토큰 : '.format(i), token)
>>> <generator object bigrams at 0x7fe4fd3b4c80>번째 토큰 : [('I', 'love'), ('love', 'twice'), ('twice', 'and'), ('and', 'NewJeans')]
>>> <generator object bigrams at 0x7fe4fd3b4e40>번째 토큰 : [('I', 'love'), ('love', 'twice'), ('twice', 'and'), ('and', 'NewJeans'),
('I', 'love'), ('love', 'twice')]
>>> <generator object bigrams at 0x7fe4fd3b4eb0>번째 토큰 : [('I', 'love'), ('love', 'twice'), ('twice', 'and'), ('and', 'NewJeans'),
('I', 'love'), ('love', 'twice'),
('I', 'like'), ('like', 'to'), ('to', 'dance')]
cfd = ConditionalFreqDist(token)
cfd.conditions() #값이 있는것만 걸러줌
>>> ['I', 'love', 'twice', 'and', 'like', 'to']
##밑에서 어떤 값인지 알아보자tabulate() 함수로 데이터프레임으로 시각화가 가능하다.
cfd.tabulate()
>>>
NewJeans and dance like love to twice
I 0 0 0 1 2 0 0
and 1 0 0 0 0 0 0
like 0 0 0 0 0 1 0
love 0 0 0 0 0 0 2
to 0 0 1 0 0 0 0
twice 0 1 0 0 0 0 0
cfd.plot()
.most_common(n번째)로 n번째로 빈도가 많은 값을 출력할 수도 있다.
print(cfd['I'].most_common(1)) #'I'와 동시출현한 빈도가 1번째로 많은거 출력
>>> [('love', 2)]
빈도수 행렬로 만들어보고, 엣지와 노드로 시각화를 해보자.
import numpy as np
freq_matrix = []
## cfd.keys() : ['I', 'love', 'twice', 'and', 'like', 'to']
for i in cfd.keys():
temp = []
for j in cfd.keys():
temp.append(cfd[i][j])
freq_matrix.append(temp)
freq_matrix = np.array(freq_matrix)
import pandas as pd
df = pd.DataFrame(freq_matrix, index=cfd.keys(), columns=cfd.keys())
df.style.background_gradient(cmap='coolwarm')

시각화
import networkx as nx
G = nx.from_pandas_adjacency(df)
print(G.nodes()) #각 단어들
>>> ['I', 'love', 'twice', 'and', 'like', 'to']
print(G.edges()) #관계가 있는것들
>>> [('I', 'love'), ('I', 'like'), ('love', 'twice'), ('twice', 'and'), ('like', 'to')]각 엣지에 접근해보면 각 엣지의 가중치에 각 단어간의 빈도가 사용된것을 확인 가능!!
print(G.edges()[('I', 'love')])
>>> {'weight': 2}
print(G.edges()[('I', 'like')])
>>> {'weight': 1}nx.draw()를 통해 간편하게 그래프를 그릴 수 있음.
nx.draw(G, with_labels=True)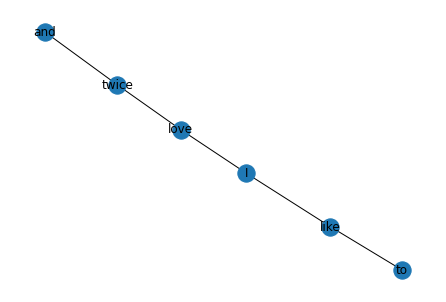
어휘 동시 출현 빈도를 계산하면 어휘 동시 출현 확률까지 측정이 가능하다.
nltk의 ConditionalProbDist를 이용하면 된다.
from nltk.probability import ConditionalProbDist, MLEProbDist
cpd = ConditionalProbDist(cfd, MLEProbDist)
##확률매트릭스로 변환
prob_matrix = []
for i in cpd.keys():
prob_matrix.append([cpd[i].prob(j) for j in cpd.keys()])
prob_matrix = np.array(prob_matrix)
print(cpd.keys())
>>> dict_keys(['I', 'love', 'twice', 'and', 'like', 'to', 0])
df = pd.DataFrame(prob_matrix, index = cpd.keys(), columns=cpd.keys())
df.style.background_gradient(cmap='coolwarm')
중심성
- 연결망 분석에서 가장 많이 주목받는 속성
- 전체 연결망에서 중심에 위치하는 정도를 표현하는 지표 : 연결정도, 중요도를 알 수 있음
구분
1. 연결(Degree) 중심성
2. 위세(Eigenvector) 중심성
3. 근접(Closeness) 중심성
4. 매개(Betweenness) 중심성
1.연결중심성
- 가장 기본적이고 직관적으로 중심성을 측정하는 지표
- 텍스트에서 다른 단어와의 동시 출현 빈도가 많은 특정 단어는 연결중심성이 높다
- 연결 정도로만 측정하면, 연결망의 크기에 따라 달라져 비교가 어려움. 여러방법으로 표준화
- 직접적으로 연결된 노드만 측정
쉽게 계산해주는 라이브러리로 계산가능 networkx
nx.degree_centrality(G)
>>>{'I': 0.4, 'love': 0.4, 'twice': 0.4, 'and': 0.2, 'like': 0.4, 'to': 0.2}
위세중심성(Eigenvector Centrality)(Ce)
- 연결된 벡터가 무조건 많다고 중요한 노드는 아니다.
- 중요한 노드와 많이 연결된 노드가 더 중요!!
ex)페북 친구가 아무리 많다고 해서 유명인사인건 아니죠. 유명인사인 친구가 많을수록 유명인사
- 연결된 상대단어의 중요성에 가중치를 둠
- 중요한 단어와 많이 연결됐다면 위세 중심성은 높아지게 됨.
- eigenvector를 구해야하므로, 직접계산은 쉽지 않음
그래도 어떻게 구하는진 알아보자.

요 행렬을 A라고 두고,

라고 가정하자. eigenvalue값을 구하고 eignevector값을 구해서 위세 중심성Ce를 구한다.
nx.eigenvector_centrality(G, weight='weight')
>>>
{'I': 0.5019050144742921,
'love': 0.6617642453275445,
'twice': 0.4941820706013397,
'and': 0.16415795399374697,
'like': 0.1874040039231038,
'to': 0.062252924445157516}
3. 근접중심성(Closeness Centrality)
- 한 단어가 다른 단어에 얼마나 가깝게 있는지를 측정하는 지표
Cc = (모든 노드 수-1) / (i노드에서 모든 노드로 가는 최단 경로 수)
nx.closeness_centrality(G, distance='weight')
>>>
{'I': 0.35714285714285715,
'love': 0.35714285714285715,
'twice': 0.2777777777777778,
'and': 0.22727272727272727,
'like': 0.3125,
'to': 0.25}
4. 매개 중심성(Betweenness Centrality)
- 한 단어가 단어들과 연결망을 구축하는데 얼마나 도움을 주는지 측정하는 지표
- 매개 중심성이 높은 단어 : 빈도수가 작더라도, 단어간 의미부여 역할이 큼.
→ 해당단어를 제거하면 의사소통이 어려워짐.
nx.betweenness_centrality(G)
>>>
{'I': 0.6000000000000001,
'love': 0.6000000000000001,
'twice': 0.4,
'and': 0.0,
'like': 0.4,
'to': 0.0}노드j에서 k로 가는 모든 최단경로중 노드i가 포함된 경로의 비율
말로 설명하기 어렵다.

페이지랭크(PageRank)
- 구글 PageRank알고리즘(논문 1998년, 구글 검색엔진의 핵심)
- 구글 230조 회사의 시작 : 세르게이 브린, 래리 페이지의 논문에서 시작(http://infolab.stanford.edu/~backrub/google.html)

- 페이지의 중요도를 웹페이지 간 연결관계에 기반을 두고 측정한 지표
- 웹페이지들을 노드로, 웹페이지에서 다른 웹페이지로 하이퍼링크를 엣지로 그래프로 나타내보자.
(B에서 C로 가는 화살표 : 웹페이지 B에 C로가는 링크를 달았다는 의미)

- 노드안의 숫자는 각 웹페이지의 중요도를 의미.
- C,E에서 알 수 있듯, 단순히 링크가 많다고 중요도가 큰건 아님.
- 인용을 한 웹페이지의 중요도가 클수록 중요도가 크다!!!
페이지랭크 알고리즘이 어떻게 되었는지 알아보자.

그래프를 위와 같이 있다고 가정하면, 인접행렬(Adjacency matrix)는 다음과 같다.
$$ \left[
\begin{matrix}
0 & 1 &1 & 1 & 0 \\
1 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 & 0 \\
1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 \\
\end{matrix}
\right] $$
확률행렬(Stochastic matrix)을 구해보자.
모든 열의 합을 1로 만드는 확률로 만든다.

이제 구글 행렬을 만들자.
'NLP' 카테고리의 다른 글
| ch4. 문서분류(Document Classification) (0) | 2023.01.24 |
|---|---|
| ch3. 군집분석 (0) | 2023.01.19 |
| ch2. 키워드 분석(KeywordAnalysis) (0) | 2023.01.19 |


